
The Mass of Jupiter
Introduction
The main goal of this lab is to give you experience putting theory into practice.
By using observations of Jupiter taken by the now retired Rigel robotic telescope formerly managed by the University of Iowa, you will determine the mass of Jupiter by applying Kepler's 3rd law.
You will also learn the power of the tool www.wolframalpha.com, which is the Google of computations. You can enter full equations with units into its search bar, and it will automatically handle all calculations!
Part 1: Kepler's Laws
Kepler's 3rd law only applies to two objects orbiting each other - like the Earth orbiting the Sun, or the moon orbiting the Earth.
It specifically links the time it takes to orbit with how far apart the objects are from each other, and how massive the objects are.
So if you can measure how far apart two objects are, and you can measure how long it takes them to orbit each other - then you can calculate their masses!
In this lab, you will measure the distance between Jupiter and one of its moons, and measure how long it takes the moon to orbit. Then using those two measurements, you will calculate Jupiter's mass.
Let's take a look at the equation for Kepler's 3rd law:
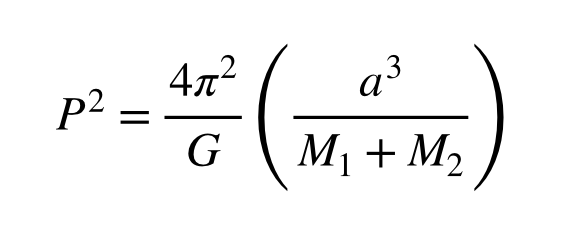
First of all - don't panic! Be patient and try to understand what's going on here - it's very simple and you CAN do it. *pom pom gets stuck in ceiling fan*
The first thing to notice is that 4π2 is just a number: 4 x 3.1415 x 3.14159 = about 39.
The next thing to notice is the letter G is also just a number - called Newton's Gravitational Constant.
In other words, those numbers are constants and we can just combine them together and replace them with one number, 5.915 x 1011:

Now, let's do an example using the Sun and the Earth to figure out how we can determine the mass of the Sun. (You will repeat this same procedure with Jupiter and one of its moons later). Start by replacing M1 and M2 with the mass of the Sun and the Mass of the Earth.

Here is where this law becomes very powerful and also very simple: because the mass of the Sun is soooooo much bigger than the mass of the Earth, adding the mass of the Sun to the mass of the earth doesn't really do anything to the equation:

The above line just says that adding the mass of the earth to the mass of the Sun gives you approximately the mass of the Sun - that squiggly equal sign means equalish.
Now the equation becomes a little bit simpler:

At this point we simply have to do two algebraic operations to solve for the mass of the Sun, exchanging a P2 for the MSun:
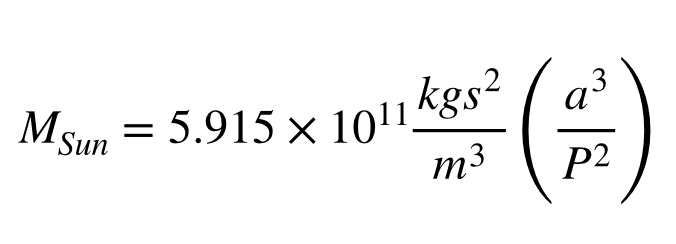
This equation is easy to solve and you can maybe almost probably calculate the mass of the Sun without looking up any of the numbers, because 'a' is the distance the Earth is from the Sun - the distance between the two masses. Do you remember what that number is?
It is 1 AU.
What about P? What do you put for P?
Remember that the Earth takes 1 year to orbit, so P is one year!
That's it, you just plug those two numbers in, 1 AU and 1 year into Kepler's 3rd law, and you can calculate the mass of the sun!
Instead of trying to convert all these units to get them to match, let's just head over to wolframalpha.com and put in the numbers with their units as is.
Be sure to pay attention to where you put the parenthesis, because order of operations is king.
PLEASE EXCUSE MY DEAR AUNT SALLY.
(You will enter this formula into wolframalpha in the same way for calculating the mass of Jupiter in part 2, replacing P and a with the values for the Jupiter/moon system.)
Check it out!

Go to wolframalpha.com and enter the above to calculate the mass of the Sun.
Pay close attention to get the parentheses right: (4 AU)2 is not the same as 4 AU2
What do you get for the mass of the sun when you enter that in? Report the answer on your worksheet for Part 1.
Part 2: Determining the Mass of Jupiter
For this part, you will use this image of Jupiter and its moons:

Your first job now is to figure out which of these moons is the moon Europa.
This is the moon you will use to measure the mass of Jupiter.
Download the image and open it with the Preview App. (Or MS Paint if you're on Windows).
Use Stellarium to label the moons, by entering the date, time, and location that the picture was taken from.
This picture of Jupiter was taken with the University of Iowa's robotic telescope called Rigel. It was operated at the Winer Observatory in Tuscon, Arizona. (This is because Arizona has mostly clear nights, whereas Iowa's nights are mostly cloudy. Rigel is retired, there's a new telescope called Gemini in current operation.)
The date and time it was taken was:
Date: 2012-03-09 Time: 03:39:20.848 UTC (UTC time is 6 hours ahead of MST.)
The time is in UTC time, so enter the date and time as shown into Stellarium, and then manually move the time back 6 hours.
We can find the period of Europa by watching it orbit Jupiter. In the following animation, we can see that it takes 3.55 days for Europa to go around Jupiter. This is the period of its orbit, P:

So now we know that the moon is Europa, that the period of orbit is P= 3.55 days, now all you need to do is determine 'a' for Kepler's Law. Remember 'a' is how far away Europa is from Jupiter.
To determine 'a', we need to use the small angle formula.
Recall that the small angle formula relates the distance to Jupiter (D), the distance Europa is from Jupiter (this is what we will use as 'a'), and the angle of separation between Jupiter and Europa.

In our image, if we simply count the pixels, we can measure the angular separation between Europa and Jupiter.
Here is an example of how I use the Preview app to count the pixels. I traced out 'a' with a blue line by clicking and dragging, in order to measure the angle ø:
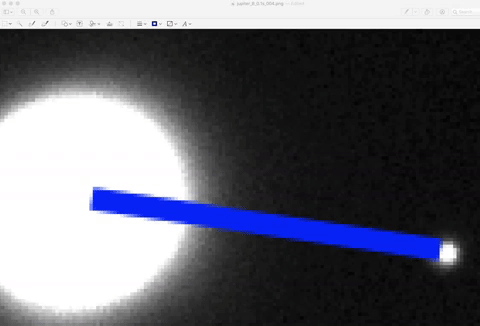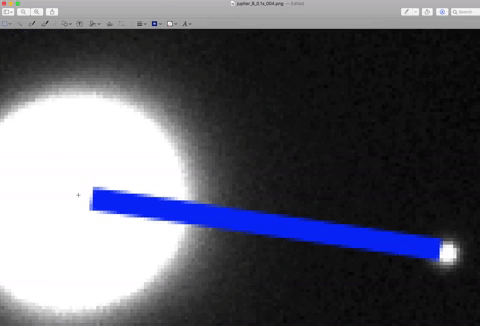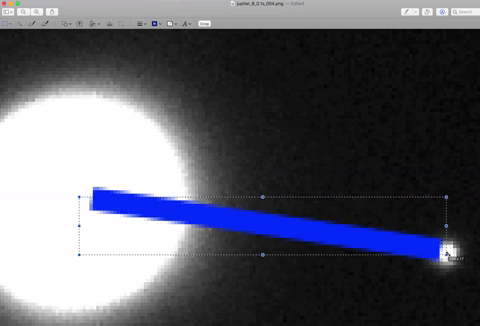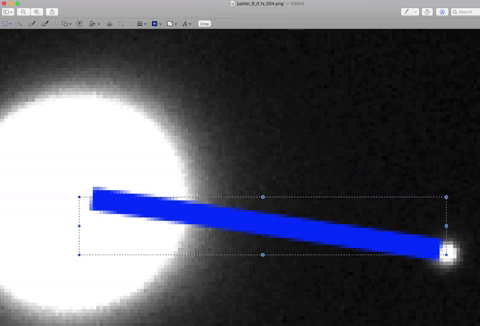
Now look closely at the rectangle I drew:

You can see the "108 x 18" - that means the rectangle I drew has dimensions of 108 pixels over and 18 pixels down.
Now, what we actually want is the hypotenuse of that triangle, to get the distance in pixels from Europa to Jupiter. So use the pythagorean theorem to do that: √(1082+182) = 109 pixels.
*NOTE: These numbers are not the correct numbers, I measured a random picture to show you how it works. You need to count the pixels yourself.
So now that I know Europa appears to be 109 pixels from Jupiter, I look up the manufacturer's specification for the camera used on Rigel - It tells us that each pixel has an angular size of 0.73" per pixel - that is 0.73 arc seconds per pixel. That's an angle!
So if we have 109 pixels, and each pixel has an angular size of 0.73 arc seconds, then the angular separation of Europa from Jupiter is 109 pixels * 0.73" per pixel = 80 arcseconds.
And LASTLY we need to convert 80 arcseconds into radians - there are 206,265 arc seconds in every radian:
80 / 206265 = 0.00038785 radians. (Now you see why we use arcseconds!)
This is 'ø', the angular separation between Jupiter and Europa.
Now let's use it to calculate 'a', the distance Europa actually is from Jupiter.
The Small Angle Formula says that:
ø = a / D
Rearranging to solve for a:
a = ø x D
a = 0.00038785 x D
The distance to Jupiter (D) when this image was taken can be found by querying wolframalpha.com with the following:
Distance to jupiter on March 9th, 2012
This will return a value in 'AU'.
Now plug in your values for 'a' and 'P' into Kepler's third law formula to get the mass of Jupiter!
Compare it with the true value and cry in awe at your power, human!
